Emiliano Rossi ID
Médico cardiólogo. Departamento de Investigación. Hospital Italiano de Buenos Aires.
Ciudad
Autónoma de Buenos Aires, Argentina.
Acta Gastroenterol Latinoam 2022;52(1):7-10
Recibido: 19/01/2022 / Aceptado:
18/03/2022 / Publicado en www.actagastro.org el
30/03/2022 / https://doi.org/10.52787/agl.v52i1.164
En un gran número de situaciones clínicas, no solo nos interesa estudiar si se presenta o no un evento, sino también determinar en qué momento del seguimiento se produce.
El análisis de sobrevida es un conjunto de procedimientos estadísticos para el análisis de datos en los cuales la variable de resultado es el tiempo hasta que un evento ocurre.
Las primeras aplicaciones de este análisis estudiaron el tiempo desde el inicio de un tratamiento hasta la muerte, de ahí el nombre de sobrevida. Posteriormente, su aplicación se extendió a otras situaciones de interés clínico (tiempo a la reinternación, al abandono del tratamiento, al retorno laboral luego de una cirugía, etc.), por lo que una denominación más adecuada es la de análisis de tiempo al evento.
Los objetivos del análisis de sobrevida son: a) estimar e interpretar la sobrevida, b) comparar la sobrevida entre distintos grupos y c) evaluar la relación de distintas variables explicativas con la sobrevida.1
Habitualmente, se estudia un solo evento de interés, aunque puede establecerse un punto final combinado (considerándose para el análisis el primer componente que se presente). En otras situaciones de mayor complejidad, se consideran eventos recurrentes o competitivos.1
Los diseños donde puede verse aplicada la metodología del análisis de sobrevida son los estudios de cohortes y los ensayos clínicos.
Para poder aplicar este análisis, se necesita determinar, al inicio del estudio, qué pacientes son susceptibles de sufrir el evento, excluyendo a aquellos que no lo son, y luego registrar la fecha en la que ocurre el evento de interés o la fecha de finalización del seguimiento en los casos en los que no se hubiera presentado.
Son dos conceptos íntimamente relacionados. La función de sobrevida S (t) es definida como la probabilidad de sobrevivir hasta un determinado tiempo. La función de riesgo h (T) es la probabilidad condicional de presentar el evento a determinado tiempo, dado que el individuo ha sobrevivido hasta ese momento.2 El gráfico de la función de sobrevida es la curva de sobrevida.
Es un concepto relevante a tener en cuenta al realizar un análisis de sobrevida. El tiempo hasta la ocurrencia del evento no es visible en todos los pacientes, está censurado porque el seguimiento se ha interrumpido (por ej. debido a pérdida de seguimiento del paciente): no hay forma de saber cuándo ocurrirá el evento a partir de ese momento. Las situaciones en las que puede haber tiempo de sobrevida censurado ocurren cuando hay pérdida de seguimiento, se produce un retiro del estudio o este finaliza y el paciente todavía no ha presentado el evento.1
La ventaja de utilizar el análisis de sobrevida es que nos permite considerar la información disponible de todos los pacientes, no solo de los que llegaron al final del seguimiento. Cada paciente aporta información durante el periodo en el que permane en el estudio, aunque luego se pierda el seguimiento. Los pacientes que presentan censura temprana contribuyen con menos información que quienes son seguidos por un largo tiempo. Todas las observaciones aportan alguna información. En cambio, si se incluyera en el análisis solo a los pacientes que finalizaron el estudio, se estaría introduciendo un sesgo.
Los métodos más conocidos que permiten manejar la censura, en un análisis de sobrevida, son las curvas de Kaplan-Meier y el modelo de riesgos proporcionales de Cox.
Las curvas de Kaplan-Meier grafican la proporción de pacientes que han sobrevivido en el tiempo en cada grupo de tratamiento (exposición). La altura de la curva de Kaplan-Meier, al final de cada intervalo de tiempo, se determina tomando la proporción de pacientes que permanecieron sin el evento al final del intervalo anterior y multiplicándola por la proporción de pacientes que sobrevivieron al final del intervalo actual. Este proceso iterativo de multiplicación de probabilidades comienza en el primer intervalo temporal y continúa hasta el último. La curva de sobrevida no se modifica al momento en el que una observación es censurada, pero en el periodo siguiente se excluye del número de personas en riesgo a las que han presentado censura.
La comparación de las curvas de Kaplan-Meier se lleva a cabo mediante el log-rank test.2 Esta prueba testea la hipótesis nula de que no hay diferencia entre las curvas de sobrevida de los distintos grupos y para ello considera los eventos observados y los esperados para cada grupo.
El modelo de riesgos proporcionales de Cox permite resolver el problema de la censura y, además, ajustar por covariables (por ej. confundidores). La medida de resumen del modelo es el hazard ratio (HR). El HR es la relación entre el riesgo (hazard) del grupo de interés y el de referencia. Nos permite estimar cuánto aumenta el riesgo de sufrir el evento por cada unidad de aumento de la variable explicativa. Por ejemplo, si el HR es 1,25 para la edad (en años), esto significa que por cada aumento de un año el individuo tiene un 25% más de riesgo de presentar el evento de interés.
Este modelo requiere que se cumplan dos supuestos.3 El primero es que los datos censurados sean independientes del resultado de interés. Esto no se cumple en el caso de pacientes que, por haber presentado el evento de interés, pierden el seguimiento. El segundo supuesto es que los riesgos sean proporcionales, es decir, que el HR sea constante durante toda la duración del estudio. Esto significa que si aumenta (o disminuye) el riesgo en el grupo expuesto, en forma concomitante debe aumentar (o disminuir) en el grupo comparador, manteniéndose constante la relación entre ambos. Si estos supuestos no se cumplen, los resultados del modelo no son válidos.
El HR no es constante cuando los efectos del tratamiento cambian en el tiempo o cuando la susceptibilidad de sufrir el evento varía entre los individuos de uno de los grupos (dándose el fenómeno de agotamiento de susceptibles).4 Estas situaciones son frecuentes en los estudios clínicos y se debe tener en cuenta que, aunque se apliquen test para evaluar la proporcionalidad de los hazards, estos pueden no tener suficiente poder.4, 5
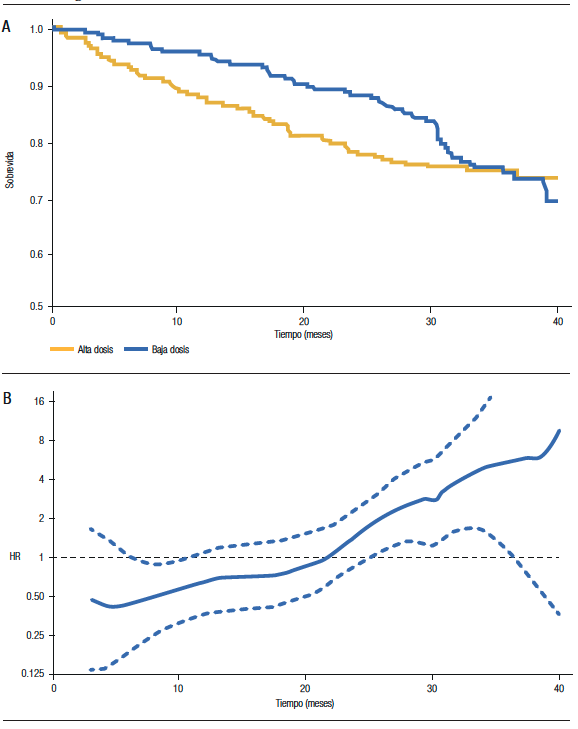
A los fines prácticos, debemos sospechar que el supuesto de proporcionalidad de los hazards no se cumple cuando las curvas de sobrevida presentan cambios manifiestos en sus pendientes. En la Figura 1A, que muestra la sobrevida de dos grupos de pacientes con mieloma múltiple tratados con bajas y altas dosis de dexametasona (ECOG Study), se observa que, en el periodo inicial, las curvas de sobrevida son divergentes. Luego tienden a ser paralelas y finalmente, convergen (llegando incluso a entrecruzarse). Si observamos el gráfico del HR a lo largo del seguimiento (Figura 1B), notamos que el HR no es constante. Inicialmente, es menor a 1 (lo que indica que el hazard del grupo baja dosis es menor), posteriormente hacia la mitad del seguimiento es igual a 1 y finalmente, es mayor a 1. El HR estimado, en este estudio, fue de 0,87, lo que no debe interpretarse como una reducción uniforme del 13% de la mortalidad para el grupo baja dosis.5
En estos casos, no debemos utilizar el HR sino otras medidas para comparar las diferencias de sobrevida entre los grupos. Una de las alternativas que disponemos es la razón de tiempo de sobrevida media restringido. El tiempo de sobrevida media restringido (RMST, según sus siglas en inglés) representa el promedio grupal de tiempo libre de eventos durante el periodo. Se calcula estimando el área bajo la curva de Kaplan-Meier hasta un tiempo determinado. En el estudio mencionado (ECOG), el RMST a 40 meses del grupo baja dosis tiene un área bajo la curva igual a 35,1 meses (lo que significa que se espera que un paciente de este grupo viva 35,1 meses de los 40 meses de seguimiento). En cambio, en el grupo alta dosis, el área bajo la curva representa 33,3 meses; siendo entonces la razón de RMST = 35,1/40 = 1,06 (IC 95% 1,00 -1,13).5
Figura 1. A) Curvas de sobrevida según tratamiento, B) Estimación del HR (y su IC 95%) durante el seguimiento.
Aviso de derechos de autor
© 2022 Acta Gastroenterológica Latinoamericana. Este es un artículo de acceso abierto publicado bajo los
términos de la Licencia Creative Commons Attribution (CC BY-NC-SA 4.0), la cual permite el uso, la
distribución y la reproducción de forma no comercial, siempre que se cite al autor y la fuente original.
Cite este artículo como: Rossi E. Introducción al análisis de sobrevida. Acta Gastroenterol Latinoam. 2022;52(1):7-10 https://doi.org/10.52787/agl.v52i1.164
Correspondencia: Emiliano Rossi
Correo electrónico: emiliano.rossi@hospitalitaliano.org.ar
Acta Gastroenterol Latinoam 2022;52(1):7-10